TransE 作用
就是把三元组翻译成embedding词向量的方法
三元组,也就是(头实体,关系,尾实体)的形式,头实体和尾实体统称为实体。为了简化起见,我们用(h,r,t)来表示三元组。其中
h表示头实体
r表示关系
t表示尾实体
我们的目标是将知识库中所有的实体、关系表示成一个低维的向量。我们把三元组(h,r,t)对应的向量表示为(h,r,t)。
h 表示头实体对应的向量
r 表示关系对应的向量
t 表示尾实体对应的向量
这样,“姚明”这个实体就不再是一个孤立的符号了,而是一个低维的稠密的向量。它看起来就像下面这样:
[0.01, 0.04, 0.8, 0.32, 0.09, 0.18]
上面这个向量的维度是6维,真实情况下向量的维度会比这个大,但具体取多大并没有一个统一的标准,一般取为50~200左右。
TransE的基本思想
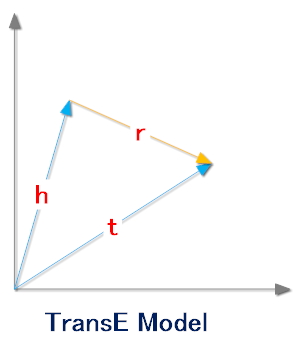
TransE模型认为一个正确的三元组的embedding向量(h,r,t)会满足公式:h+r=t
头实体embedding加上关系embedding会等于尾实体embedding。
如果是一个错误的三元组,那么它们的embedding之间就不满足这种关系。
TransE的目标函数
目标是学得所有实体和关系的embedding。
理想情况下,一个正确的三元组的embedding之间会有h+r=t的关系,而错误的三元组之间不会有这个关系。
因此我们定义如下的势能函数:$$ f(h,r,t) = ||h+r-t||_2 $$
通过h和r之和与t之差的二范数来表示这个三元组的势能。
二范数:
$$ ||\textbf{x}||2 =\sqrt{\sum{i=1}^Nx_i^2} $$
Euclid范数(欧几里得范数,常用计算向量长度),即向量元素绝对值的平方和再开方。
对于一个正确的三元组,我们希望势能越低越好,而对于一个错误的三元组,我们希望势能越高越好。这样我们就很容易给出目标函数了:
$$ min\sum{(h,r,t)\in\Delta} \sum{(h^{‘},r^{‘},t^{‘})\in\Delta}[\gamma + f(h,r,t) - f(h^{‘},r^{‘},t^{‘})]_+ $$
其中
$\Delta$ 表示正确的三元组集合
$\Delta^{‘} $表示错误的三元组集合
$\gamma$ 表示正负样本之间的间距,是一个常数
$[x]_+$ 表示max(0,x)
为了方便训练,避免过拟合,通常还会在上述目标函数后面增加约束条件
||h||≤1,||r||≤1,||t||≤1。
负样本(错误三元组)的产生
通常我们得到的知识库是三元组的集合,所有在知识库中出现了的三元组都被看作是正例,那我们如何产生负例呢?我们通常使用替换法来获取负例。
对于三元组(h,r,t)
我们随机用知识库中的某个实体h′来替换h,或者用某个实体t′来替换t,这样我们就得到了两个负例(h′,r,t)和(h,r,t′)。
为了避免出现生成的负例其实存在于知识库中的情况,我们可以对生成的负例进行过滤,如果它是知识库中的正例,那我们就不把它作为负例,而是重新生成一个负例。
transE评价方法
transE得到每个实体和关系的embedding之后,如何评估这些学得的embedding的质量—-Link prediction。
这个方法不仅可以用于评估transE,但凡是评估embedding的质量,都可以用这个评估方法。
基本的评价过程
假设整个知识库中一共有n个实体,那么评价过程如下:
- 将一个正确的三元组a中的头实体或者尾实体,依次替换为整个知识库中的所有其它实体,也就是会产生n个三元组。
- 分别对上述n个三元组计算其能量值,在transE中,就是计算h+r-t的值。这样可以得到n个能量值,分别对应上述n个三元组。
- 对上述n个能量值进行升序排序。
- 记录三元组a的能量值排序后的序号。
- 对所有的正确的三元组重复上述过程。
- 每个正确三元组的能量值排序后的序号求平均,得到的值我们称为Mean Rank。
- 计算正确三元组的能量排序后的序号小于10的比例,得到的值我们称为Hits@10。
有两个指标:Mean Rank和Hits@10。
其中Mean Rank越小越好,Hits@10越大越好。
改进
上述过程存在一个不合理的地方:在将一个正确的三元组a的头或者尾实体替换成其它实体之后得到的这个三元组也有可能是正确的,在计算每个三元组的能量并排序之后,这类正确的三元组的能量有可能排在三元组a的前面。但是上面所说的基本评价过程并没有考虑这点。因此我们把上述基本评价过程得到的结果称为Raw Mean Rank和Raw Hits@10,把改进方法得到的结果称为Filtered Mean Rank和Filtered Hits@10。
为了更好的评价embedding的质量,我们对上述方法进行改进。
- 将一个正确的三元组a中的头实体或者尾实体,依次替换为整个知识库中的所有其它实体,也就是会产生n个三元组。
- 分别对上述n个三元组计算其能量值,在transE中,就是计算h+r-t的值。这样可以得到n个能量值,分别对应上述n个三元组。
- 对上述n个能量值进行升序排序。
- 记录三元组a的能量值排序后的序号k。
- 如果前k-1个能量对应的三元组中有m个三元组也是正确的,那么三元组a的序号改为k-m。
- 对所有的正确的三元组重复上述过程。
- 每个正确三元组的能量值排序后的序号求平均,得到的值我们称为Filtered Mean Rank。
- 计算正确三元组的能量排序后的序号小于10的比例,得到的值我们称为Filtered Hits@10。
算法局限和进阶
虽然 TransE 模型具有训练速度快、易于实现等优点,但是它不能够解决多对一和一对多关系的问题。以多对一关系为例,固定 r 和 t,TransE 模型为了满足三角闭包关系,训练出来的头节点的向量会很相似。
该模型已经成为了知识图谱向量化表示的 baseline,并衍生出不同的变体:TransH ,TransR ,TransD ,CTransR ,TransA 等等
References
知识表示-TransE
TransE论文:多元关系数据嵌入
Translating Embeddings for Modeling Multi-relational Data
